히스테리시스 곡선

이번 포스팅은 전기 이론 부분에서 

변압기 등의 철심재료로 많이 사용되는 강자성체의 히스테리시스 현상에 대해 알아보려 합니다.

 

1. 히스테리시스 곡선​

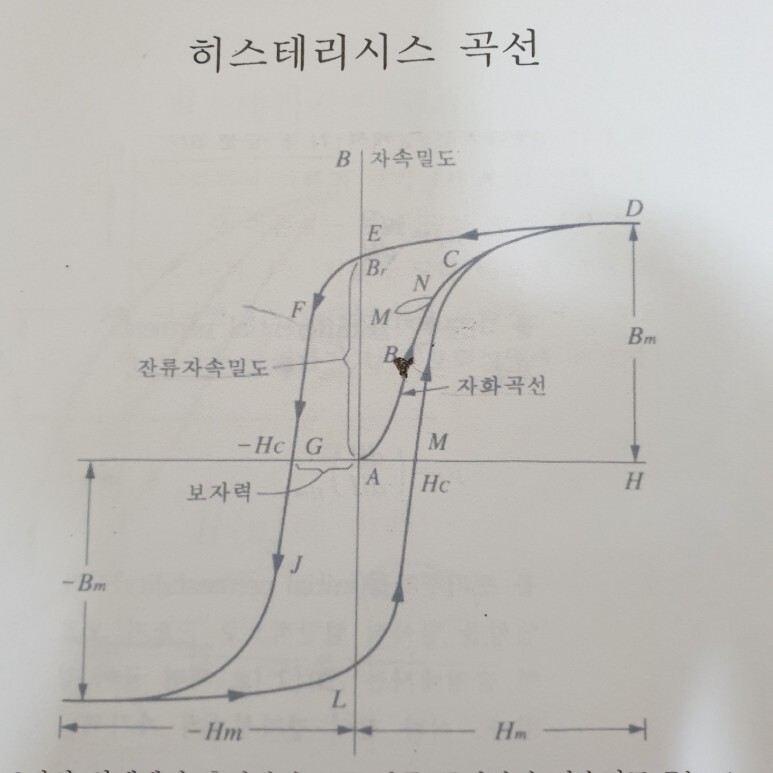
그림에서와 같이 원점의 상태에서 출발하여 H(자계)를 차츰 증가하면 자속밀도 B는 A->B->C->D 라는 자화 곡선을 그리고고 D점에 이르러 포화 상태에 이르게 됩니다. 이 포화 상태는 모든 자기 영역이 정렬되어 더 이상 자화 되지 않습니다.

​

다음은 H를 역으로 감소시키면 B는 D->E 이동하여 H 값이 0이 되어도 E 점에서 주어진 값을 가집니다.

E 점에서의 자속밀도 Br을 잔류자기 하고 합니다.

​

다음으로 H를 더욱 역방향으로 증가하면 곡선은 E->F->G 와 같이 되고 GA에 해당하는 역방향으로 H가 가해졌을 때 B의 값은 0이 되는데 G 점에 해당하는 자계의 세기 Hc를 보자력이라고 합니다.

​

H를 더욱 증가 시키면 P 점에 대해서 대칭인 L인 점에서 잔류 자기, M 점의 보자력을 경유해서 D 점에 돌아와 하나의 루프를 그리게 됩니다.

이것을 히스테리시스 환선 또는 히스테리시스 루프라 합니다.

 

추가적으로 설명하면 이 히스테리시스 곡선을 통해 다음과 같은 사항을 파악할 수 있습니다

자성체에 인가된 자기장을 지속적으로 증가시켰을 때 도달하게 되는 포화 자속밀도,

​

인가 자계를 제거하였을 때 남아있는 잔류자속밀도,

​

자성체에 남아있는 잔류자속밀도를 제거하기 위한 역 자기장의 세기인 보자력

(보자성 자계),

​

그리고 B=pH 이므로 히스테리시스 곡선의 접선 기울기인 해당 자성체의 투자율,

​

마지막으로 히스테리시스 곡선의 내부 면적인 히스테리시스 손실을 알 수가 있습니다

 

아래 그림에서 설명을 추가하면

​

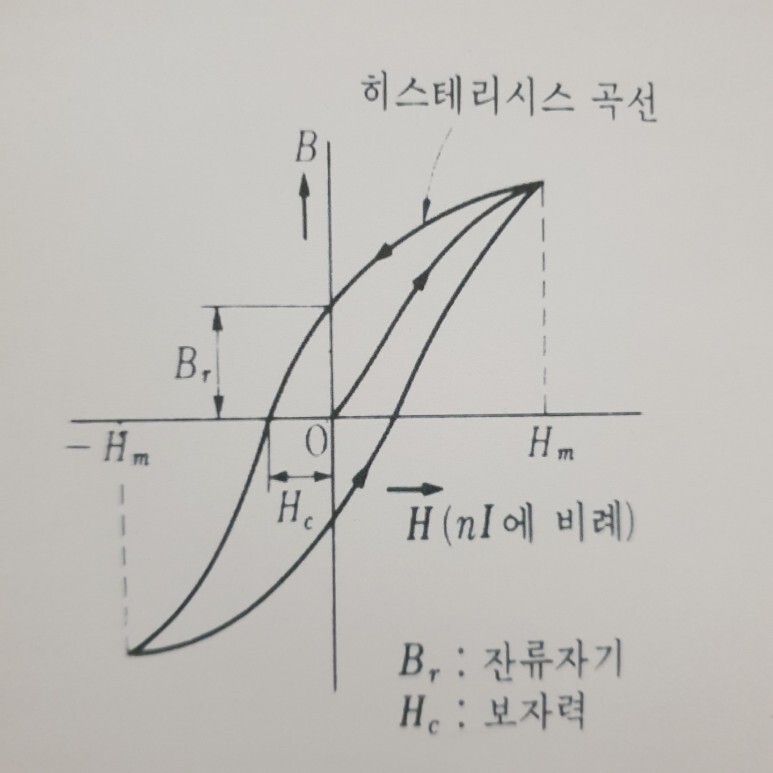
철심(강자성체)을 자화하는 경우에, 자기장의 세기(자속밀도, H)의 변화 철심의 자계의 세기(B)의 변화가 초기 자화곡선과 일치하지 않고 그림과 같이 고리 모양으로 곡선을 이룹니다..

일반적으로 외부적인 힘에 의한 어떤 물체의 성질 변화가 변화의 원인이 제거된 이후에도 쉽사리 본래의 상태로 되돌아가지 않는 현상을 히스테리시스라 하며, 위의 곡선을 히스테리시스 루프(histeresis loop)라 합니다.

​

2. 히스테리시스 손실(hysteresis loss)

히스테리시스 곡선으로 둘러싸인 면적은 단위 체적당의 에너지 손실을 나타내며

수식은 아래와 같습니다.

Ph = ηfBm1.6

여기서,

η 히스테리시스 상수, f 주파수(Hz), Bm 최대 자속밀도

​

3. 전기기기의 철심

히스테리시스 손실을 줄이기 위하여 전기기기에 사용되는 철심에는 규소(Si)가 함유된 철심을 성층으로 하여 사용한다

(주로 변압기의 경우)

​

여담으로 히스테리란

우리가 보통 히스테리 부린다 하는데 여기서 히스테리는 독일어로

심리 정신적 원인에 의해서 일시적으로 일어나는 비정상적인 흥분상태를 통틀어 이르는 말이며

​

즉 히스테리시스란

물질의 물리량이 현재의 물리적 조건만으로 결정되지 아니하고 이전부터 그 물질이 겪어온 상태의 변화 과정에 의하여 결정되는 현상을 말합니다.

강자성체의 자화나 탄성의 변형 따위에서 찾아 볼수 있습니다.

그런 의미에서 히스테리시스 부리는 금속물로 이해하면 될듯합니다.